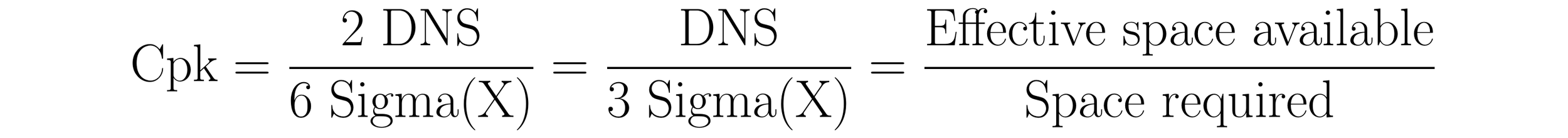Centered Capability Ratio, Cpk
The centered capability ratio, Cpk, divides the DNS by the quantity 3Sigma(X). Thus, it expresses the effective space available to a process as a multiple of the space required when the process is operated at its current mean. By comparing the centered capability ratio with the capability ratio, a characterization of how far off-target a process is operating is revealed. As the two ratios converge, the closer a process is operating to on-target. As the two ratios diverge, the further a process is operating from on-target.
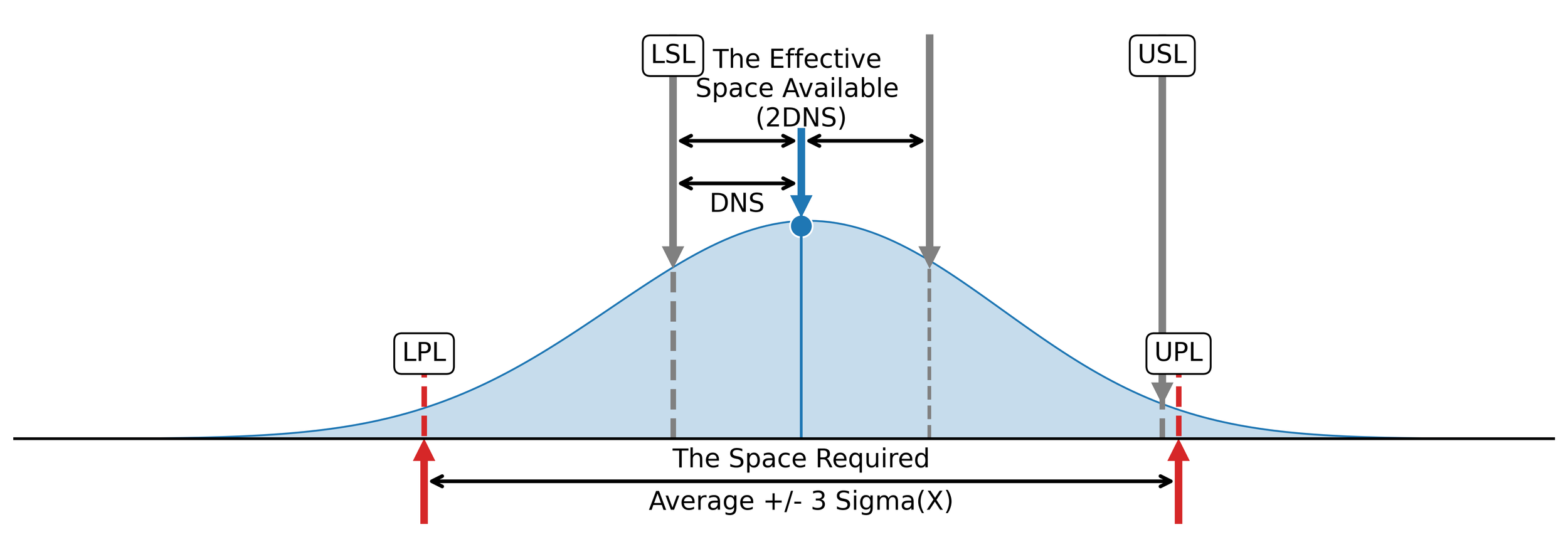
The relationship between the effective space available and the space required is further clarified in Figure 1. Here, a generic distribution of individual values is shown in the context of the specification limits (the space available), the effective space available (2DNS), and the process limits (the space required). Note that the distribution in Figure 1 is bias toward the Lower Specification Limit (LSL), not centered. This bias towards the LSL is as if the process is operating within specification limits that have a width equal to 2DNS instead of the space available.
Figure 1. The relationship between the effective space available and the space required.
When a process is operated in the middle of the specification limits (on-target), the centered capability ratio and the capability Ratio will converge (rarely will the values be the same). As the process mean deviates from the target, the centered capability ratio will be smaller than the capability ratio. Thus, the value of the centered capability ratio relative to the capability ratio reveals how close to target a process is operating. As the values converge, the closer to on-target the process is operating. As the values diverge, the further from on-target the process is operating.
A word of warning
The centered capability ratio, like all process parameters, is not well-defined until the underlying causal system is operated predictably. Whenever a process is operated unpredictably, that is it is influenced by both common causes of routine variation and assignable causes of exceptional variation, the process parameters, including the process mean, the process standard deviation, and the process capability indices, will change over time. While we can always compute statistics regardless of the characterization (predictable or unpredictable), the only time this arithmetic can be used to estimate process parameters is when the process is operated predictably. When a process is operated unpredictably “the process parameters are changing and are therefore divorced from the statistics” used to calculate them (Wheeler, More Capability Confusion, 2).
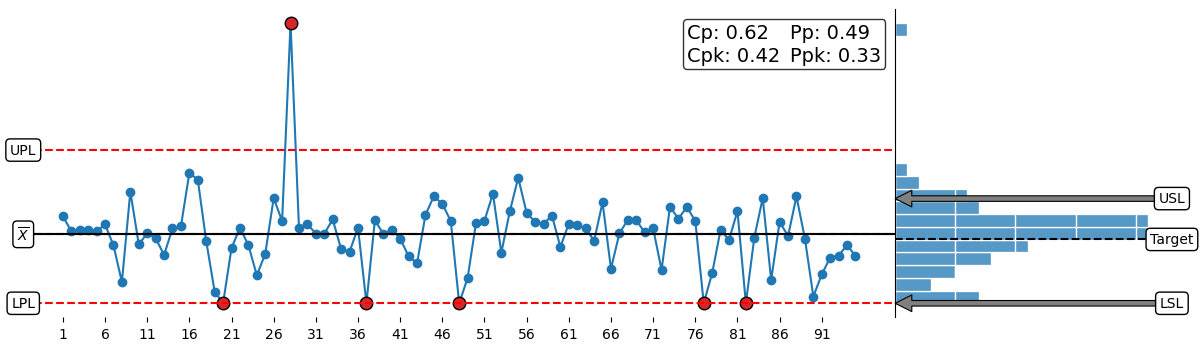
It is for the above reasons that the process capability indices should always be reported with the additional context of a process behavior chart and a capability histogram. The process behavior chart will characterize process behavior as predictable or unpredictable and, in doing so, reveal the voice of the process. The capability histogram will visualize the relationship between the specification limits (tolerance) and the process data. In doing so, the capability histogram reveals the relationship between the process data and the voice of the process.
Figure 2. The X chart portion of an XmR chart (left) and the associated capability histogram (right).